The image recorded by a camera depends on three factors: The physical content of the scene, the illumination incident on the scene, and the characteristics of the camera. This leads to a problem for many applications where the main interest is in the physical content of the scene. Consider, for example, a computer vision application which identifies objects by colour. If the colours of the objects in a database are specified for tungsten illumination (reddish), then object recognition can fail when the system is used under the very blue illumination of blue sky. This is because the change in the illumination affects object colours far beyond the tolerance required for reasonable object recognition. Thus the illumination must be controlled, determined, or otherwise taken into account.

The ability of a vision system to diminish, or in the ideal case, remove, the effect of the illumination, and therefore "see" the physical scene more precisely, is called colour constancy. There is ample evidence that the human vision system exhibits some degree of colour constancy (see, for example, [MMT76, BW92, Luc93]). One consequence of our own color constancy processing is that we are less aware of colour constancy problems which face machine vision systems. These problems become more obvious when dealing with image reproduction. For example, if one uses indoor film (balanced for tungsten illumination) for outdoor photography, one will get a poor result. The colour change is much larger than we would expect, based on our experience of looking at familiar objects, such as a friend’s face, both indoors and out.

This leads us to the relationship between colour constancy and image reproduction. The main thesis here is that illumination modeling is also beneficial for image reproduction and image enhancement. In the above example, taking a good picture required selecting the film based on the illumination. However, choosing among a limited number of film types provides only a rough solution, and has the obvious limitation that human intervention is required. Digital image processing yields opportunities for improved accuracy and automation, and as digital imaging becomes more prevalent, the demand for image manipulation methods also increase. Often modeling the scene illumination is a necessary first step for further image enhancements, as well as being important for standard image reproduction.

To complete the argument that modeling scene illumination is necessary for image reproduction, we must consider the interaction of the viewer with the reproduction. For example, one may ask why the viewer does not remove the blue cast in a reproduction, much as they would remove a blue cast due to blue light in the original scene. First, note that failing to remove the cast from the reproduction is consistent with the claim that humans exhibit colour constancy. This is because colour constancy is by definition the reduction of the effect of the scene illumination, which is the illumination present when the reproduction is viewed, not the illumination present when the picture was taken. Thus, the empirical result is that the viewing experience is sufficiently different in the two cases that human colour constancy functions according to the definition. The most obvious difference is that scenes occupy the entire visual field whereas reproductions do not. However, even if a reproduction occupies the entire visual field, the viewer will still not remove a blue cast due to incorrect film type. It is possible to identify many other ways that the two viewing experiences differ, and the characterization of the relevant differences is a subject of ongoing research. To summarize, since the human viewer compensates for the viewing illumination, but not the illumination present when the image was taken, image reproduction must compensate for this scene illumination.

Naturally, this is only the beginning of the story. For example, a completely illumination invariant photographic system would not be able to "see" mountains painted red by a setting sun. Here the effect of the illumination is very much a part of the photograph. Nonetheless we expect a perfect image capture system to be cognizant of the overall illumination, because it is relevant to us whether the alpenglow is especially red, or alternatively, white, with the rest of the scene being especially blue, as would be suggested if we were to use indoor film to capture the scene. Thus for automated high quality reproduction, illumination modeling is still an obvious starting point. Similarly, for computer vision applications the goal is not to ignore illumination effects, but to separate them from the overall image signal. For example, a shadow contains information about the world which we want to use, but we also want to recognize that the shadow boundary is not a change in scene surface.

To emphasize the connections between image reproduction and computer vision, imagine a vision system which is able to determine the physical characteristics of the scene, and thus implicitly the illumination. Using this information, we can now reproduce the scene as it would be appear under any illumination, including the original illumination. This is suggestive of image enhancement, which can be defined as image processing which leads to an image which is, in some sense, more appropriate for human viewing. An example of image enhancement which may be approached through illumination modeling is dynamic range compression. Here the problem is that the range of intensities in natural images far exceeds that which can be reproduced linearly with inexpensive technologies. This wide range of intensities is largely due to the wide range of illumination strengths. For example, printed media cannot linearly represent the intensities in a bright outdoor scene and a dark shadow therein. A vision system which can recognize the shadow as such can be used to create an enhanced reproduction where the shadow is reproduced as less dark. Illumination modeling is required here because mistakenly applying the same processing to a dark surface is undesirable.

It may be argued that the image enhancement example above is actually an example of image reproduction, because the human experience of the scene may involve a less dark shadow–certainly it involves seeing the detail in the shadow. Regardless of the best categorization of the application, it should be clear that proceeding effectively requires an adequate model of human vision, which itself is intimately linked with our research area. One may argue that adequate models of human vision might be obtainable by mere measurement, but one popular point of view, which I think is valuable to pursue, is that a complete understanding of the human vision system requires an understanding of what computational problems are being solved [Mar82]. This point of view brings us back to computer vision, which is largely inspired by human abilities, and the philosophical stance that those abilities can be viewed as the result of computation.

In summary, I claim that modeling scene illumination is central to the recovery of facts about the world from image data, which inevitably has the scene illumination intertwined with the information of interest. Furthermore, progress in modeling the scene illumination will result in progress in computer vision, image enhancement, and image reproduction. In what follows, I will first discuss the nature of image formation and capture, and then, in the rest of the paper, I will overview the computational approaches that have been investigated so far, as well as their applications.

Modeling illumination on the basis of an image (or a sequence of images), can be viewed as inverting the image formation process. Thus it is essential to look at the relationship between the world and the images in a forward direction. The main conclusion that we will draw is that determining the illumination from an image is inherently very under-constrained, and thus making progress in our quest requires making intelligent assumptions about the world.

We begin with a digital image, which is a sampling of a light signal traditionally modeled by a continuous function of wavelength and geometric variables. In the case of a colour image, we have three samples which are ostensibly centered over the same location. For our purposes, the nature of the spatial sampling is not critical, and I generally will ignore the associated issues. On the other hand, we are quite interested in the sampling of the input with respect to wavelength. In general, the response of image capture systems to a light signal, , associated with a given pixel can be modeled by:

(1)

where is the sensor response function for the kth channel, is the kth channel response, and is the kth channel response linearized by the wavelength independent function . In this formulation, absorbs the contributions due to the aperture, focal length, sensor position in the focal plane. This model has been verified as being adequate for computer vision over a wide variety of systems (see, for example, [ST93, HK94, Bar95, VFTB97a, VFTB97b] and the references therein). This model is also assumed for the human visual system (see for example [WS82]), and forms the basis for the CIE colorimetry standard. Here, are linear transformations of the colour matching functions, are the X, Y and Z colour coordinates, and is taken to be the identity function.

In the common case of three camera channels, is the linearized red channel, hereafter designated by R, is the green channel, designated by G, and is the blue channel designated by B. Often we wish to ignore the brightness information in the sensor response. In the usual case of three sensors, this is done by mapping the three dimensional RGB responses into a two dimensional chromaticity space. There are numerous ways to do this. The most common is the mapping r=R/(R+G+B) and g=G/(R+G+B). This will be referred to as the rg chromaticity space. Another mapping, used in the two dimensional gamut mapping algorithms described below is given by (R/B, G/B).

The continuous functions in (1) are normally approximated by a sequence of measurements at successive wavelengths. For example, the commonly used PR-650 spectraradiometer samples spectra at 101 points from 380nm to 780nm in 4nm steps with each sampling function being approximately 8nm wide. Thus it is natural and very convenient to represent them as vectors, with each component being a sample. Using this representation, (1) becomes:

(2)

This notation emphasizes that image capture projects vectors in a high dimension space into a N-space, where N is 3 for standard colour images. This means that image capture looses a large amount of information, and recovery of the spectra from the vision system’s response is not possible. Put differently, many different spectra have exactly the same camera response. For human vision in reasonably bright conditions, N is also three, and again, many different spectra will be seen as the same colour. This forms the basis of colour reproduction. Rather than attempt to reproduce the spectra of the scene’s colour, it is sufficient to create a spectra which has the same response, or, equivalently, has the same projection into the three dimensional sensor space.

I will now discuss the formation of the input signal, designated by above, along the lines in [Hor86] and [LBS90]. is the result of some illuminant signal interacting with the surface being viewed. Since the interaction is linear it is natural to define the reflectance of the surface as the ratio of the reflected light to the incident light. This ratio is a function of the direction of the illumination, the direction of the camera, and the input and output polarization which I will ignore for the moment. This gives us the bi-directional reflectance function (BDRF), defined as the ratio of the image radiance in the direction of the solid angle due to the surface irradiance from (see Figure 1):

(3)

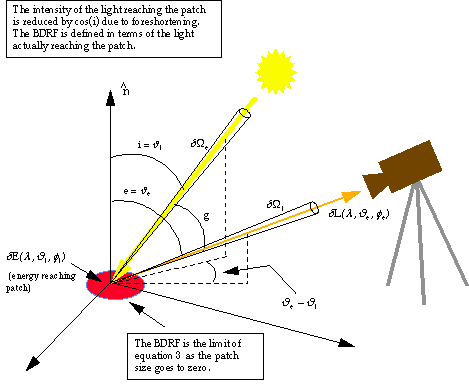
Given the BDRF, we can express the signal from a surface in the more realistic case of multiple extended light sources by:

(4)

The reflectance of most surfaces does not change significantly if the surface is rotated about the surface normal. Such surfaces are referred to as isotropic. In this case the BDRF can be simplified to or, more commonly, , where the third variable is now the angle between the viewing and illuminant directions.

One important limitation of the BDRF is that is inappropriate for fluorescent surfaces. In the case of fluorescence, a surface absorbs energy at one wavelength, and emits some of that energy at a different wavelength. Since the interaction is linear for any pair of input and output wavelengths, the BDRF now becomes . So far, fluorescence has been largely ignored in computer vision, likely because of the difficulties it presents. In the case of human vision, preliminary work suggests that a sufficiently fluorescent surface is perceived as self-luminous [PKKS]. Finally, if we wish to extent the BDRF to include polarization, then we need to add an input polarization multi-parameter, and an output polarization multi-parameter. This complete model of reflection is referred to as the light transfer function in [MS97].

Since the BDRF is a function of three (isotropic case) or four geometric parameters, measuring the BDRF for even one surface is very tedious. Nonetheless, some such data has become available for a variety of surfaces [DGNK96]. However, it is clear that we need simpler models, and that the main importance of the measured data is for testing our models, rather than being used directly. I will now discuss some of the models that have been developed.

The simplest possible form of the BDRF is a constant. This corresponds to perfectly diffuse reflection, also referred to as Lambertian reflection. A Lambertian reflector appears equally bright, regardless of the viewing direction. If the Lambertian reflector reflects all energy incident on it without loss, then it can be shown that [Hor86].

In computer vision it is common to forgo the BDRF in favour of the reflectance factor function [NRH+74, LBS90], which expresses the reflectance of a surface with respect to that of a perfect diffuser in the same configuration. This is closer to the usual method of measuring reflectance which is to record the reflected spectrum of both the sample and a standard reflectance known to be close to a perfect diffuser. The reflectance factor function is then the ratio of these two. In order to keep the two expressions of reflectance distinct and to maintain consistency with the literature, I will denote the reflectance factor function by . This leads to the most common form of the imaging equations:

(5)

The simplicity of Lambertian reflectance makes it an attractive approximation for modeling reflectance, but unfortunately, it is a poor model in many cases. Investigating the physics of reflectance leads to better models. One very useful idea is the dichromatic model proposed for computer vision in [Sha85]. This model has two terms corresponding to two reflection processes. Specifically, the light reflected from a surface is a combination of the light reflected at the interface, and light which enters the substrate and is subsequently reflected back as the result of scattering in the substrate. These two reflection components are referred to as the interface reflection and the body reflection. Furthermore, for most non-metallic materials, the interface reflection is only minimally wavelength dependent, and thus light reflected in this manner has the same spectra as the illuminant. On the other hand, the scattering processes that lead to the body reflection are normally wavelength dependent.

Formally, then, the dichromatic model for a surface reflectance is given by:

(6)

where is the interface reflectance (usually assumed to be a constant), is the body reflection, and and are attenuation factors which depend on the geometry developed above (see Figure 1). A key simplification offered is the separation of the spectral and geometric effects. Several research have carried out experiments testing the efficacy of this model in the context of computer vision [Hea89, TW89, LBS90, Tom94b].

The body reflection is often assumed to be Lambertian. In the case of smooth dielectrics, a detailed analysis indicates that this is a good approximation, provided that the angles e and i in Figure 1 are less than 50o [Wol94]. In the case of rough surfaces, Lambert’s law breaks down, even if the material itself obeys Lambert’s law. The effect of surface roughness on the body reflection is modeled in [ON95].

Surface roughness also affects specular reflection. Two approaches to modeling this effect are surveyed in [NIK91]. The first is based on physical optics (Beckmann-Spizzichino) and the second uses geometric optics (Torrance-Sparrow). Physical optics is exact, but requires approximations and simplifications due to the nature of the equations. Geometric optics is simpler, but requires that the roughness is large compared to the wavelength of light under consideration. Both methods require some specification of the statistical nature of the roughness. The analysis in [NIK91] leads to the proposal of three contributions to reflection: The body reflection, the specular lobe, and the specular spike, which is normally only present for very smooth surfaces. Thus this analysis extends the dichromatic idea by splitting one of the reflection processes into two.

A similar model can be developed in the case of metals [Hea89]. Metals have no body reflection, and the interface reflection is often quite wavelength dependent, explaining the colour of metals such as gold and copper. The proposed model again separates the spectral and geometric effects. The efficacy of such a monochromatic model is tested in [Hea89], and is found to be reasonable.

I will now discuss models for the wavelength dependence of surface reflection, as well as illuminant spectral distribution. Although many of the physical process involved are known, physics based models appropriate for computer vision have yet to be developed. However, statistical models have been studied extensively and have proven to be very useful. The general method is to express a data set as a linear combination of a small number of basis functions. In the case of a surface reflectances we have:

(7)

Here are the basis functions and are the projections. Similarly, for illuminants we have:

(8)

If a set of spectra is well approximated by N basis functions, then that set will be referred to as N-dimensional. Such models work well when the spectra of interest are smooth, and thus quite band limited. This seems to be good assumption for surface reflectances, as several large data sets of surface reflectances have been successfully modeled using such models [Coh64, Mal96, PHJ89, VGI94]. For example, in [PHJ89] the spectra of 1257 Munsell color chips were fit to 90% with 4 basis functions, and to 98% with 8 basis functions. The number of basis functions required to fit daylight is even smaller [JMW64, Dix78]. Dixon [Dix78] found that for a daylight data set taken at one location, three basis functions accounted for 99% of the variance, and for another data set, four functions accounted for 92% of the variance. It should be noted that the spectra of a number of artificial lights, including fluorescent lights, are not smooth, and when such lights need to be included, the approximation in (8) is less useful.

The basis functions are normally determined from data sets of spectra using either singular value decomposition, or occasionally by principal component analysis, where the mean is first subtracted from the data set. The singular value decomposition is usually applied to the spectra directly, but in [MW92] it is argued that the basis functions should be found relative to the vision system sensors. In short, the standard method is sub-optimal because it will reduce errors fitting spectra to which the vision system has little sensitivity at the expense of spectra which need to be well approximated. Thus [MW92] propose using the responses directly to find basis functions for surface reflectances or illuminants (one-mode analysis). In the usual case that the responses are produced by both reflectance and illuminant spectra, two-mode analysis is used, which requires iteratively applying one-mode analysis to obtain estimates of the surface reflectance bases and the illuminant bases (convergence is guaranteed).

Finite dimensional models allow image formation to be modeled compactly using matrices. For example, assuming three dimensional surface reflectance functions, we can define a lighting matrix for a given illuminant by:

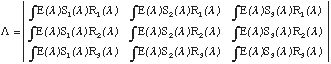(9)

Then for a surface , the response is given simply as:

(10)

Consider two images of the same scene under two different illuminants. For example, Figure 2 shows a ball in front of a green background taken under two illuminants, a tungsten illuminant for which the camera is well balanced, and simulated deep blue sky. Now, a priori based on (5), each pixel RGB is affected differently by the illumination change. However, there is clearly a systematic response as well–under the bluer light, all pixels seem to tend towards blue. In this section I will discuss models for the systematic response, as it is this response is the key to progress.

To aid in the presentation, I will now introduce some notation. In order to be consistent with the gamut mapping approaches described below, I will always describe mappings from the image of a scene taken under a unknown illuminant, to that taken under a known illuminant. Following Forsyth [For90], the known illuminant will also be referred to as the canonical illuminant. Quantities specific to the unknown illuminant will be super-scripted with U, and quantities specific to the canonical illuminant will be super-scripted with C.

One common simple model of illumination change is a single linear transformation. Thus each pixel of the image taken under the unknown illuminant, , is mapped to the corresponding pixel of the image taken under the canonical illuminant, , by , where M is single 3 by 3 matrix used for all pixels. Such a model can be justified using the finite (specifically, 3) dimensional models discussed above. From (10) we can estimate and which gives the estimate , and thus M above is given explicitly by: It should be noted that due to a number of factors, the linear transformation model of illumination change can easily be more accurate than the finite dimensional models used to justify it. More to the point, the transformation does not need to be the best possible M for our particular scene, illuminant pair, and camera sensors.

If we restrict M above to be a diagonal matrix, we get an even simpler model of illumination change. Such a model will be referred to as the diagonal model. The diagonal model maps the image taken under one illuminant to another by simply scaling each channel independently. For concreteness, consider a white patch in the scene with response under an unknown illuminant and response under a known canonical illuminant . Then the response of the white patch can be mapped from the test case to the canonical case by scaling the ith channel by . To the extent that this same scaling works for the other, non-white patches, we say that the diagonal model holds.

The diagonal model has a long history in colour constancy research. It was proposed by von Kries as a model for human adaptation [Kri1878], and is thus often referred to as the von Kries coefficient rule, or coefficient rule for short. This model has been used for most colour constancy algorithms. The limitations of the model itself have been explored in [WB82, Wor85, WB86, Fin95]. In [WB86], West and Brill discuss how the efficacy of the diagonal model is largely a function of the vision system sensors, specifically whether or not they are narrow band, and whether or not they overlap. The relationship is intuitively understood by observing that if the sensors are delta functions, the diagonal model holds exactly. In [Wor85] it is pointed out that the use of narrow band illumination, which has a similar effect to narrow band sensors, aids the colour constancy observed and modeled in the well known Retinex work [MMT76, Lan77].

In [FDF94a], Finlayson et al propose the idea of using a linear combination of the vision system’s sensors to improve the diagonal model. If the vision system sensors are represented by the columns of a matrix, then the new sensors are obtained by post multiplying that matrix by the appropriate transform T. An important observation is that if camera responses are represented by the rows of a matrix R, then the camera response to the new, modified sensors, is also obtained by post multiplication by T. The main technical result in sensor sharpening is finding the transformation T. Three methods for finding T are proposed: "sensor based sharpening", "database sharpening", and "perfect sharpening". Sensor based sharpening is a mathematical formulation of the intuitive idea that narrower band (sharper) sensors are better. Database sharpening (discussed further below) insists that the diagonal model holds as well as possible in the least squares sense for a specific illumination change. Finally, perfect sharpening does the same for any illumination change among a set of two dimensional illuminants in a world of three dimensional reflectances.

In database sharpening, RGB are generated using a database of reflectance spectra, together with an illuminant spectrum and the sensors. This is done for two separate illuminants. Let A be the matrix of RGB for the first illuminant and B be the matrix for the second, with the RGB’s placed row-wise. In the sharpening paradigm we map from B to A with a sharpening transform, followed by a diagonal map, followed by the inverse transform. If we express each transform by post multiplication by a matrix we get: . In database sharpening the matrix T (and implicitly D) is found that minimizes the RMS error, . T is found by diagonalizing M, where M minimizes . Thus the sharpening transform gives exactly the same error as the best linear transform M, and therefore, for a specific illumination change, the diagonal model is equivalent to the a priori more powerful full matrix model. This notion is explored in detail in [FDF94b].

In summary, the diagonal model is the simplest model of illumination change that gives reasonable results. As will become clear below, its simplicity supports many algorithms by keeping the number of parameters to be estimated small. It should be noted that since overall brightness is often arbitrary in colour constancy, the number of parameters is often one less than the number of diagonal elements. In general, the error incurred in colour constancy is a combination of parameter estimation error, and the error due to the model of illumination change. Intuitively, the error due to parameter estimation increases with the number of parameters. With current colour constancy methods, the error in parameter estimation in the case of diagonal model algorithms is still large compared to the error due to diagonal model itself, especially when the camera sensors are sufficiently sharp, or when sharpening can be used (see [Bar95] for some results). Thus it would seem that there is little to recommend using models with more parameters than sensors (less one, if brightness is considered arbitrary).

So far I have been discussing the simple case that the illumination is uniform across the image under consideration. However, the above generalizes easily to the case where the illumination varies, as any given model of illumination change must apply locally. Thus in the case of varying illumination, we have an entire spatially varying field of mappings. This means that the diagonal model is sufficient because we now model the illumination change of each image sample independently. Formally, in the usual case of three sensors, each response is mapped to by a diagonal matrix specific to that response: .

As discussed in the introduction, the goal of computational colour constancy is to diminish the effect of the illumination to obtain data which more precisely reflects the physical content of the scene. This is commonly characterized as finding illuminant independent descriptors of the scene. However, we must insist that these descriptors carry information about the physical content of the scene. For example, computing a field of zeros for every image is trivially illuminant independent, but it is useless.

One we have an illumination independent description of the scene, it can be used directly for computer vision, or it can be used to compute an image of how the scene would have looked under a different illuminant. For image reproduction applications, this illuminant is typically one for which the vision system is properly calibrated. It has proved fruitful to use such an image itself as the illuminant invariant description [For90, Fin95, Bar95, Fin96]. Ignoring degenerate cases, illuminant invariant descriptions can be inter-converted, at least approximately. However, the choice of invariant description is not completely neutral because it is normally more accurate to directly estimate the descriptors that one is interested in. This often leads us to prefer using the image of the scene under a known, canonical illuminant as the illuminant invariant description. In the case of image reproduction this should be clear, as we are typically interested in how the scene would have appeared under an illuminant appropriate for the vision system. It is equally the case in computer vision, if only because most computer vision algorithms developed so far assume that the there is an illuminant–and typically ignore the problem that it may change. Specifically, computer vision algorithms tend to work on pixel values, and thus implicitly assume both illumination and sensors are involved, as opposed to assuming that some other module delivers some abstract characterization of the scene. This makes sense, because such a characterization will have error, and thus it is preferable to use the raw data. An example is object recognition by colour histograms [SB91]. Here, a database of colour histograms of a variety of objects is computed from images of these objects. Since we know the illuminant used to create the database, a natural choice of descriptors is how the objects would appear under this known illuminant. Other choices can be made, perhaps with certain advantages, but likely at the expense of some error.

Many algorithms have been developed to find the illuminant invariant descriptions discussed above. The most prominent ones will be discussed below. Since the problem is under constrained, making progress requires making some additional assumptions. The algorithms can be classified to some degree by which assumptions they make, and the related consideration of where they are applicable.

The most important classification axis is the complexity of the illumination, and the most important division is whether or not the illumination is uniform across the image. A second important classification axis is the whether the algorithm is robust with respect to specular reflection or the lack thereof. Some algorithms require the presence of specular reflections, others are neutral with respect to them, and some are degraded by them. Most algorithms assume that the illumination is uniform, and that there are no specularities. This has been referred to as the Mondrian world, since the collections of matte papers used in the Retinex experiments were likened to paintings by Mondrian (this likeness is debatable). Finally, some algorithms attempt to recover a description which is only invariant with respect to illuminant chromaticity, ignoring illuminant brightness. It should be clear that any algorithm which recovers brightness can be used as an algorithm to recover chromaticity by simply projecting the result. Also, any algorithm used to recover chromaticity can be used together with a estimate of brightness to be compared with algorithms which recover both. I will now discuss the most prominent approaches in the context of these classifications.

Perhaps the simplest general approach to colour constancy is to compute a single statistic of the scene, and then use this statistic to estimate the illumination, which is assumed to be uniform in the region of interest. An obvious candidate for such a statistic is the mean, and this leads to the so called grey world assumption. In physical terms, the assumption is that the average of the scene reflectance is relatively stable, and thus is approximately some known reflectance which is referred to as grey. Although this is a very simple approach, there are a number of possible variations. One distinction is the form of the specification of the grey. Possibilities include specifying the spectra, the components of the spectra with respect to some basis, and the RGB response under a known, canonical illuminant. A second, more important, distinction, is the choice of the grey. Given a method for specifying the grey, the best choice would be the actual occurrence of that grey in the world. However, this quantity is not normally available (except with synthetic data), and thus the choice of grey is an important algorithm difference.

One approach is to assume that the grey is in fact grey; specifically, the reflectance spectra is uniformly 50%, or that it has the same RGB response as if it were uniformly 50%, assuming the diagonal model of illumination change. Using the diagonal model, the algorithm is to normalize the image by the ratio of the RGB response to grey under the canonical illuminant, to that of the average image RGB. A related method is to use the average spectra of a reflectance database to obtain the RGB of grey, instead of assuming uniform reflectance.

Buchsbaum used a grey world assumption to estimate a quantity analogous to the lighting matrix defined in (9) [Buc80]. However, as pointed out by Gershon et al [GJT88], the method is weakened by an ad hoc choice of basis, as well as the choice of grey, which was set to have specific, equal, coefficients in the basis. Gershon et al improved on the method by computing the basis from a database of real reflectances, and using the average of the database as the reflectance of their grey. The output of the algorithm is estimates of the coefficients of the surface reflectances with respect to the chosen basis. As touched upon above, for most applications, it is likely to be better to directly use the camera response as descriptors, and if this algorithm were modified in this manner, then it would become the last algorithm described in the previous paragraph.

Gershon et al recognized that exact correspondence between their model and the world requires segmentation of the image so that the average could be computed among surfaces as opposed to pixels. In their model, two surfaces should have equal weight, regardless of their respective sizes. The reliance on segmentation would seem to be problematic because segmentation of real images is difficult, but I will argue that this algorithm should degrade gracefully with respect to inaccurate segmentation. This is because the result from any segmentation corresponds to the result with perfect segmentation for some possible physical scene under the same illuminant (my observation–the paper does not analyze this). To see why this is the case, lets first look at an inappropriate merge of regions. The average of the single resultant region is exactly the same as a mix of the two regions seen from sufficiently far away, and thus sampled differently. For example, we may not be able to segment the green, yellow, and red leaves in a autumn tree, but the average of the incorrectly segmented blob is no different in terms of input to the algorithm than a similar tree seen at a distance. The case of erroneous splitting also corresponds to the proper segmentation of a possible scene. Specifically, a scene where the surfaces of the original scene have been split up and reorganized. Of course, as the segmentation improves, the results of the algorithm should also improve, but the results should always be reasonable.

An important contribution to colour constancy is the Retinex work of Land and his colleagues [LM71, MMT76, Lan77, Lan83, Lan86a, Lan86b] and further analyzed and extended by others [Hor74, Bla85, Hur86, BW86, FDFB92, McC97]. The original aim of the theory is a computational model of human vision, but it has also been used and extended for machine vision. In theory, most versions of Retinex are robust with respect to slowly spatially varying illumination, although testing on real images has been limited to scenes where the illumination has been controlled to be quite uniform. Nonetheless, the varying illumination component of this work is both interesting and important. In Retinex based methods, varying illumination is discounted by assuming that small spatial changes in the responses are due to changes in the illumination whereas large changes are due to surfaces changes. The goal of Retinex is to estimate the lightness of a surface in each channel by comparing the quantum catch at each pixel or photoreceptor to the value of some statistic–originally the maximum– found by looking at a large area around the pixel or photoreceptor. The ratios of these quantities (or their logarithms) are the descriptors of interest, and thus the method implicitly assumes the diagonal model. The details vary in the various versions of Retinex.

In [MMT76, Lan77] the method is to follow random paths from the pixel of interest. As each path is followed, the ratio of the response in each channel for adjacent pixels is computed. If the ratio is sufficiently close to one, then it is assumed that the difference is due to noise, or varying illumination, and the ratio is treated as exactly one. If, on the other hand, if the ratio is sufficiently different from one, then it is used as is. The ratios are then combined to determine the ratio the response of the pixel of interest to the largest response found in the path. Finally, the results for all the paths are averaged.

The above is simplified by using the logarithms of the pixel values. With this representation, the essence of the matter is differentiation (to identify the jumps), followed by thresholding (to separate reflectance from illumination), followed by integration (to recover lightness), and various schemes have been proposed to formulate Retinex as a calculus problem [Hor74, Bla85, Hur86, FDB92].

In [Lan83, Lan86a] Land also used differences in logarithms with thresholding, to remove the effect of varying illumination, together with the random path idea. However, the lightness estimate was changed to the average of the differences after thresholding. As before the result for a number of paths was averaged. In [Lan86b], the estimate was simplified even further to the logarithm of the ratio of the response of a given pixel to a weighted average of the responses in a moderately large region surrounding the pixel. The weighting function used was the inverse distance from the pixel of interest. In [Hur86], a method to solve Horn’s Poisson equation corresponding to Retinex can be approximated by a similar simple estimate, but the weighting function is now a Gaussian which is applied after logarithms are taken. Finally, in [MAG91], Moore et al change the Gaussian to , as convolution with this kernel can be achieved using a resistive network, and thus is appropriate for their hardware implementation of Retinex.

If the illumination is assumed to be uniform, then the first version of Retinex discussed above amounts to simply scaling each channel by the maximum value found in the image. Similarly, the second method discussed converges to normalizing by the geometric mean [BW86], and thus it is essentially a grey world algorithm (as is the third method). Thus Retinex can be simply and more powerfully implemented if the illumination is assumed to be uniform.

An especially elegant method for computing surface descriptors from an image was proposed by Maloney and Wandell [MW86, Wan87]. This approach is based on the small dimensional linear models discussed above. Assuming that illuminants are N dimensional and surfaces are N-1 dimensional, where N is the number of sensors, the sensor responses under a fixed, unknown light will fall in an N-1 dimensional hyper-plane, anchored at the origin. The orientation of this plane indicates the illumination. Unfortunately, in the usual case of three sensors, this method does not work very well [FFB95, BF97] which is not surprising, as the dimensionality of surfaces is more than two, and the dimensionality of illuminants can easily be more than 3 if fluorescent lighting is a possibility. Further analysis of the Maloney-Wandell method, as well as an extension for the case where the same scene is captured under multiple lights is provided by D’Zmura and Iverson [DI93].

The gamut mapping approach was introduced by Forsyth [For90], and has recently being modified and extended by Finlayson [Fin95]. These approaches explicitly constrain the set of possible mappings from the image of the scene under the unknown illuminant to the image of the scene under the known, canonical, illuminant. Although Forsyth’s analysis included both diagonal and linear maps, his most successful algorithm, CRULE, and all subsequent extensions have been restricted to diagonal maps.

One source of constraints is the observed camera responses (image pixels). The set of all possible responses due to all known or expected surface reflectances, as seen under a known, canonical illuminant, is a convex set, referred to as the canonical gamut. Similarly, the set of responses due to a unknown illuminant is also a convex set. Assuming the diagonal model of illumination change, the two gamuts are within a diagonal transformation of each other. The canonical gamut is known, but since the illuminant is unknown, we must use the observed sensor responses in the input image as an estimate of the unknown gamut. Since this estimate is a subset of the whole, there are a number of possible mappings taking it into the canonical gamut. Each such map is a possible solution, and the main technical achievement of the algorithm is calculating the solution set. A second part of the algorithm is to choose a solution from the set of possibilities. Since this algorithm delivers the entire feasible set of solutions, it has the advantage that it provides bounds on the error of the estimate. I will now provide some of the details for the computation of the solution set.

First, it is important that the gamuts are convex. A single pixel sensor may sample light from more than one surface. If we assume that the response is the sum of the responses of the two contributing pieces, and that the response due to each of these is proportional to their area, then it is possible to have any convex combination of the responses. Thus the gamut of all possible sensor responses to a given light must be convex.

Since the gamuts are convex, they will be represented by their convex hulls. Now consider the RGB’s in the image taken under an unknown light. The convex hull of these RGB’s will be referred to as the measured gamut. The measured gamut must be a subset of the unknown gamut, and since we are modeling illumination changes by diagonal transforms, each of these measured RGB’s must be mapped into the canonical gamut by the specific diagonal transform corresponding to the actual illumination change. It can be shown that a diagonal transform which maps all measured gamut hull vertices into the canonical gamut will also map the non-vertex points into the canonical gamut. Thus only the measured gamut vertices need to be considered to find plausible illumination changes.

Figure 3 illustrates the situation using two-dimensional triangular sets for explanatory purposes. Here triangle "abc" represents the convex hull of the measured RGB’s. A proposed solution must map it into the canonical gamut represented by triangle "ABC". Reiterating the above, a proposed solution must map "a" into the canonical gamut (and similarly "b" and "c").

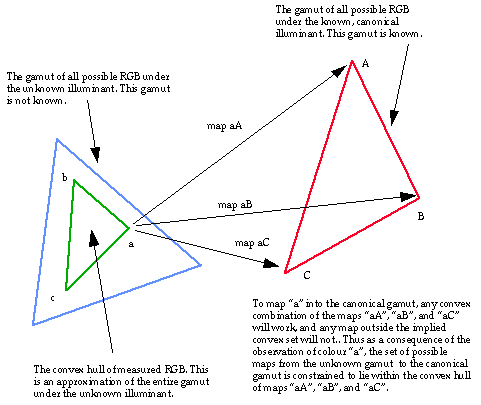
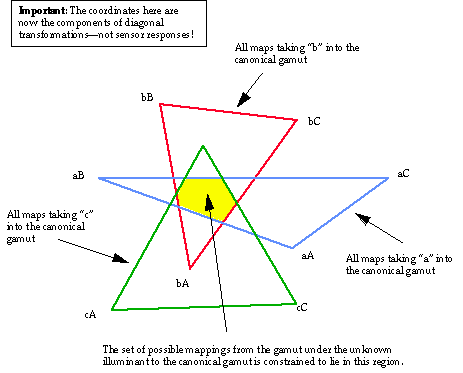
Now the set of maps which take a given point (e.g. "a") into some point in the canonical gamut is determined by the maps that take that point into the hull points of the canonical gamut. If we use vectors to represent the mappings from the given point to the various canonical hull points, then we seek the convex hull of these vectors. It is critical to realize that we have introduced a level of abstraction here. We are now dealing with geometric properties of the mappings, not the gamuts. It is easy to verify that it is sufficient to consider the mappings to the hull points (as opposed to the entire set), by showing that any convex combination of the maps takes a given point into a similar convex combination of the canonical hull points.

The final piece of the logical structure is straightforward. Based on a given point ("a" in our example), we know that the mapping we seek is in a specific convex set. The other points lead to similar constraints. Thus we intersect the sets to obtain a final constraint set for the mappings. Figure 4 illustrates the process.

Recently Finlayson proposed using the gamut mapping approach in chromaticity space, reducing the dimensional complexity of the problem from three to two in the case of trichromats [Fin95]. Not all chromaticity spaces will work. However, Finlayson showed that if the chromaticity space was obtained by dividing each of two sensor responses by a third, as in the case of (R/B, G/B), then convexity is maintained where required. One advantage to working in a chromaticity space is that the algorithm is immediately robust with respect to illumination intensity variation. Such variation is present in almost every image, as it originates from the ubiquitous effects of shading and extended light sources. Furthermore, specular reflections do not present problems because the resultant chromaticity is the same as that of the same surface with some added white.

In addition to using chromaticity space, Finlayson added an important new constraint. Not all theoretically possible lights are commonly encountered. From this observation, Finlayson introduced a constraint on the illumination. The convex hull of the chromaticities of the expected lights makes up an illumination gamut. Unfortunately, the corresponding set of allowable mappings from the unknown gamut to the canonical gamut is not convex (it is obtained from taking the component-wise reciprocals of the points in the above convex set). Nonetheless, Finlayson was able to apply the constraints in the two dimensional case. In [Bar95] the convex hull of the non-convex set was found to be a satisfactory approximation for an extensive set of real illuminants.

Unless the image has colours near the gamut boundaries, the set of possible diagonal transforms can be large enough that choosing a particular solution is an important second stage of the gamut mapping approach. In [For90], the mapping which lead to the largest mapped volume was used. In [Fin95], this method of choosing the solution was maintained in the case of two dimensional mappings used in the chromaticity version. In [Bar95], the centroid of the solution set was used, both in the chromaticity case and in the RGB case. The centroid is optimal if the solutions are uniformly distributed and a least squares error measure is used. However, in the two dimensional case, a uniform distribution of the solutions is not a good assumption because of the distorted nature of the specific chromaticity space. This lead Finlayson and Hordley to propose finding the constraint sets in two dimensions, and perform the average in three dimensions [FH98]. They justify this method by showing that under reasonable conditions, the constraint set delivered by the two and three dimensional versions is the same.

Bayesian statistics has been applied to the colour constancy problem [BF97]. In Bayesian colour constancy, one assumes knowledge about the probability of occurrence of illuminants and surface reflectances. Furthermore, each illuminant and surface combination leads to an observed sensor response, and an illuminant together with a scene leads to a conjunction of observed sensor response. If we let y be the observed sensor responses, and let x contain parameters describing proposed illuminant and scene reflectances, then Bayes’s method estimates P(x) by:

(11)

Since we are only interested in choosing x, and not the actual value of , the denominator can be ignored. Once the estimates for have been computed, a value for x must be chosen. One natural choice is the x corresponding to the maximum of . However, if this maximum is an isolated spike, and a second slightly lower value is amidst other similar values, then intuitively, we would prefer the second value, because choosing it makes it more likely that we have a value that is close to the actual value in the face of measurement error. A common method to overcome this problem is to use a loss function which gives a penalty as a function of estimation error. Such a function may be convolved with to yield the loss as a function of estimate, which is then minimized. Loss functions are discussed in detail in [BF97] which also includes the introduction of the new local mass loss function which is felt appropriate for the colour constancy application.

Bayesian colour constancy as described in [BF97] has a number of problems. First, the number of parameters is a function of the number of surfaces, and so the method is very computationally expensive. Second, their calculation of P(x) from illuminant and surface distributions assumes that the surfaces are independent, which implies that the image is properly segmented. If the image pixels are used instead, then the surfaces are not independent, as neighbours tend to be alike. Finally, the required statistical distributions of the world are not well known, and thus there is likely to be large discrepancies between simulation and real applications. In [BF97] the authors only test on synthetic scenes, which are generated according to the model assumed, and thus the performance is good.

Some of these problems are elegantly addressed with colour by correlation [FHH97], although an estimate of prior probability distributions is still required. Colour by correlation is a discrete implementation of the Bayesian concept. More importantly, the method is free from the complexities of implicitly estimating surface parameters. In colour by correlation, the probability of seeing a particular chromaticity, given each expected possible illuminant, is calculated. Then this array of probabilities is used, together with Bayes’s method, to estimate the probability that each of the potential illuminants is the actual illuminant. Finally, the best estimate of the specific illuminant is chosen using a loss function.

The colour by correlation method is related to Finlayson’s chromaticity version of gamut mapping ("Colour in Perspective") [Fin96]. First, since the algorithm chooses an illuminant among the expected ones, Finlayson’s illumination constraint is built in. Second, a specific version of colour by correlation can be seen as quite close to the colour in perspective algorithm [FHH97].

Recently good results have been achieved using a neural net to estimate the chromaticity of the illuminant [FCB96, FCB97, CFB97, CFB98]. Here a neural net is trained on synthetic images randomly generated from a database of illuminants and reflectances. The scenes so generated may include synthetically introduced specularities [FCB97]. In the work reported so far, rg chromaticity space is divided into discrete cells and the presence or absence of any image chromaticity within each of the cells is determined. This binary form of a chromaticity histogram of an image is used as the input to the neural network. During training the input corresponding to the generated scenes is presented to the network together with the correct answer. Back-propagation is used to adjust the internal weights in the network so that it thus learns to estimate the illuminant based on the input.

If a surfaces obeys the dichromatic model discussed above, then the observed RGB responses to that surface under a fixed illumination will fall in a plane. This is because the possible colours are a combination of the colour due to the body reflection, and the colour due to the interface reflection, with the amounts of each being a function of the geometry. Mathematically, the kth sensor response, , can be expressed as:

(12)

which becomes:

(13)

and using vector notation becomes:

(14)

Thus the possible RGB responses, , are a linear combination of the interface RGB, , and the body RGB, , and thus lie in a plane through the origin.

In the case of dielectrics, the interface function, , is a constant, and thus the colour due to the interface reflection is the same as the illuminant, . If two or more such surfaces can be identified with different body reflections, then the RGB of each will fall into a different planes, and those planes will intersect in the illuminant direction . A number of authors have proposed colour constancy algorithms based on this idea [Lee86, DL86, TW89, TW90, Tom94a, Ric95]. An obvious difficulty is recognizing the surfaces as such. If the observed RGB are projected onto an appropriate two-dimensional chromaticity space such as rg chromaticity, then the projected points for the surfaces present become line segments which intersect at a common point, specifically the chromaticity of the illuminant. Starting from each colour edge point found by conventional means, Lee [Lee86] collects pixels in the direction of the greatest gradient in the green channel, until another edge point is reached. Each such collection of pixels gives an estimate of a line segment, and an estimate of the intersection points of the line segments is used as the final illuminant chromaticity estimate. A slightly different approach is to look directly for the structure of lines convergent on a point in chromaticity space [Ric95].

The colour histograms due to dichromatic reflection have additional structure which may be exploited to identify such surfaces or highlights. Given a specific viewing geometry, highlights occur at a narrow range of surface normals, and thus combine with a specific amount of body reflection. Therefore the histograms consist of a line through the origin for the body reflection, together with a branch for the specular reflection departing from the colour of the body reflection at the particular angle where specular reflection occurs–the so called "dog-leg" [KSK87, GJT87]. Further analysis reveals that the specular part of the histogram spreads out where it meets the body part, the degree of spreading, accompanied by a shortening of the specular segment, being a function of the surface smoothness. Finally, the location of the merging of the two parts is a function of the viewing geometry [KSK90, NS92]. In [KSK90], Klinker et al use these finer points of the histogram structure for the combined segmentation and illumination determination of images of dielectrics.

Nayar et al [NFB93] manage to dodge the inherent segmentation problem by using polarization together with analysis of the observed colour along the lines discussed above. Polarization is an effective tool because specular reflection from dielectrics has different polarization than the body reflection.

Another method which is less dependent on segmentation, since it can work on a single region segmented very conservatively, is provided in [Lee90]. Here, the difference in the nature of the spatial variation of the specular and diffuse illumination is exploited. Specifically, specular illumination is expected to vary much more rapidly, and Lee fits a one parameter model, derived from the dichromatic model, which maximizes the smoothness of the diffuse illumination. The method can combine the results from multiple regions, again, with conservative segmentation. It should be noted, however, that this promising method has only been tested on synthetic data. A related approach is to fit the observed RGB of a surface to a Lambertian model using robust statistics [Dre94].

Finally, one general difficulty with methods based on specularities should be mentioned. Specularities tend best to reveal the colour of the illuminant where they strongly reflect that illuminant. This means that such specular regions tend to be very bright, often exceeding the dynamic range of a camera, and are thus unusable.

If we have access to images of the same scene under two or more illuminants, then we have more information about the scene and the illuminants. To see this, suppose we are trying to recover 3 parameters for both the surfaces, and the illuminants, that there are M surfaces in the scene, and that we have 3 camera sensors. Then, one image presents us with 3+3M unknowns, and 3M measurements. However, two images presents us with 6+3M unknowns, but 6M measurements. Assuming that the unknowns are not overly correlated, this is clearly a more favorable situation.

As already mentioned above, D’Zmura and Iverson [DI93] have extended the Maloney-Wandell algorithm for this circumstance. In addition, Tsukada and Ohta worked with the equations implied in the preceding paragraph in the case of two surfaces [TO90]. This yields 12 measurements to estimate 12 parameters, which become 10 parameters if brightness is normalized. Unfortunately, 3 of the measurements are quite correlated with the others, so the method is not particularly stable. The stability of the method can be improved by restricting the illuminant to CIE daylight [OH94].

The illumination falling on scenes often varies spatially due to the interaction of different illumination sources with the three dimensional world. For example, consider a white ball lying on a sunlit lawn. Part of the ball faces the sun, and receives mostly the yellow illumination of the sun, with some contribution from the blue sky. As we move around the ball, the contribution from direct sun becomes less, and the distinctly blue contribution from the sky becomes more extreme. In the self-shadowed part of the ball, the illumination is purely that from the sky. As a further example, near the lawn, the ball is also illuminated by light reflected from the lawn which is green in colour.

If we can identify a surface which is illuminated by varying illumination, then we have a situation similar to the time varying illumination case discussed in the preceding section. Specifically we have the response of that surface under more than one light. Thus we potentially have more data available to solve for the illumination. It should be clear that any algorithm based on multiple views can be modified to exploit the varying illumination. However, despite the fact that varying illumination is common, there are very few algorithms designed to exploit the extra information available.

As mentioned earlier, Retinex based methods discard slowly spatially varying illumination, thus achieving some robustness in this case, but they do not exploit the varying illumination. In [FFB95], Finlayson et al provide an algorithm along the lines of [For90, Fin96], but for the varying illumination chromaticity case. Using the observation that the chromaticities of illuminants are restricted, the authors show that the magnitude of the illuminant chromaticity changes can be used to constrain the actual illuminant chromaticity. For example, suppose common illuminants are less blue than some maximal blue, denoted by B. Now suppose that going from point X to point Y, the amount of blue doubles. Then the amount of blue at X can be at most one half B. If it were to exceed one half B, then the amount of blue at Y would exceed B, and this would break the assumption that the scene is illuminated by common illuminants.

In [FFB95], a limited set of illuminants was used, and the gamut of the reciprocals of their chromaticities was approximated by a straight line. Furthermore, no attempt was made to identify the varying illumination. In [Bar95, BFF97] a more comprehensive set of illuminants was used. In addition, the algorithm was modified so that it could be used in conjunction with the gamut mapping algorithms developed for the uniform illumination case [For90, Fin96]. The idea here is that once the varying illumination has been identified, the image can be mapped to one which has uniform illumination, and thus provides constraints on the illumination due to the surfaces. These constraints are used in conjunction with the constraints found due to the varying illumination.

Also in [Bar95, BFF97] a method was introduced to identify the varying illumination in the case of slowly varying illumination. The method is based on the assumption that small spatial changes are due to illumination changes (or noise), and that large changes are due to changes in surfaces. Using this assumption, a conservative segmentation is produced. A perfect segmentation is not needed. Specifically, it does not matter if regions of the same surface colour are combined, or if some regions are split, although too many spurious segments will degrade the recovery of the illumination. Given the segmentation, the varying illumination within a segment is easily determined, and a method is provided to robustly combine these variations into an estimate of the varying illumination field for the entire image.

A special case of varying illumination is mutual illumination. Mutual illumination occurs when two surfaces are near each other, and each reflect light towards the other. For example, consider an inside corner which is the meeting of a red surface and a blue surface, illuminated by a white light. Then the red surface near the corner will be somewhat blue near the junction due to the reflection of the white light from the nearby blue surface. Similarly, the blue surface will also have some added red near the junction.

If mutual illumination can be recognized, then it can be exploited for colour constancy. For example, Funt et al [FDH91] showed that if the mutual illumination between two surfaces could be identified as such, then this effectively added a sensor to the Maloney-Wandell algorithm, potentially increasing its efficacy. And in [FD93] the authors exploit the observation that the colours of a surface exhibiting mutual illumination are a linear combination of the two-bounce colour and the one-bounce colour. Two such planes due to a pair of mutually reflecting surfaces will intersect along the two-bounce colour, and using this information it is possible to solve for the one-bounce colours, and subsequently to constrain the no-bounce colour (the colour of the illuminant).

An important application of colour constancy processing is for illumination invariant object recognition, and its weaker cousin, image indexing. Image indexing treats images as the objects to recognized, with the canonical task being finding a test image in a database of images. As discussed in the introduction, both these problems are sensitive to the illumination, and the performance of corresponding algorithms increases with effective removal of illumination effects. To remove the illumination, any of the methods discussed above can be used. However, algorithms have also been developed which take advantage of the nature of the task. Specifically, these algorithms look for known objects, and thus they exploit knowledge about what they are looking for. I will now discuss some of these algorithms.

In [MMK94], Matas et al model each of the objects in their test database under the range of expected illuminations. Modeling known objects in the presence of a variety of expected illumination conditions is also used in [BD98]. In [MMK94] each surface on a specific object is represented by a convex set of the possible chromaticities under the range of possible illuminations. The occurrence of a chromaticity in this range is a vote for the presence of the object. In this manner, the likelihood of the presence of each object can be estimated. In [MMK95] the authors integrate colour edge adjacency information into their object recognition scheme, and use Nayar and Bolle’s [NB92] intensity reflectance ratio as an illumination invariant quantity in each of the three channels. This invariant is based on the assumption that the illumination is usually roughly constant across a boundary, and under the diagonal model the RGB ratios will be a constant across the junction of a given surface pair. To avoid problems with small denominators, Nayar and Bolle defined their reflectance ratio as (a-b)/(a+b) instead of (a/b).

Image indexing is simpler than these general object recognition approaches because it avoids the difficult problem of segmenting objects from the background. Image indexing can be used for object recognition and localization by exhaustively matching image regions. This clearly requires indexing to be fast and robust with respect to the inclusion of background as well as pose and scale. Nonetheless, the original work [SB91] was proposed as an object recognition strategy based on overcoming these difficulties. This method matched images on the basis of colour histograms. As the colour histogram of an image is dependent on the illumination, Funt and Finlayson [FF91, FF95] proposed an illumination invariant version based on matching histograms of the ratios of RGB across surface boundaries. The histograms are computed directly (without segmentation) from the derivative of the logarithm of the image, after values close to zero have been discarded. Another illumination invariant approach is to simply "normalize" both the images in the database, and the test image [FCF96, DWL98, FSC98]. Under the diagonal model, the image is scaled by the RGB of the illuminant. Any normalization of the RGB which coincides with the scaling due to the illuminant will be illumination invariant. For example, the image may be normalized by the average RGB. This is like using the grey world algorithm, but now, because of the image indexing context, the "world" is precisely known–it is the image.

As discussed in the introduction, effective illumination modeling provides the opportunity to reproduce an image as though the illumination was different when the picture was taken. Specifically, if an image is too dark in a shadowed region for a given reproduction technology, then it could be reproduced as though the shadow was less strong. Unfortunately, algorithms to explicitly model the illumination are not yet effective enough for this task. Hence algorithms have been developed which attempt to enhance the contrast of such images without requiring a complete illumination model. Two such methods are based on combining Retinex methods at various scales [FM83, JRW97]. The method in [FM83] is based on the form of Retinex where random paths are followed in order to compare the lightness of the current pixel to the maximal lightness that can be found [MMT76, Lan77]. In this work, however, the paths not random. Instead, they are chosen for efficient implementation, and the result for a given pixel is more influenced by nearby pixels than distant ones. This is the basic multi-scale idea, also used in [JRW97]. This second method is based on the form of Retinex which compares the ratio of the RGB’s of a given pixel, to that of a weighted average of surrounding pixels [Lan86]. Like that version of Retinex, the logarithm of these ratios is used as output, but unlike that version, the weighting function is a Gaussian. The idea in [JRW97] is to combine the results at different scales, which corresponds to using different sigmas for the Gaussians. Three scales are found to be adequate for their purposes.

The effect of combining small scale results into the overall result is that some colour constancy processing is now done on a local area, and thus these methods can now, to some extent, deal with varying illumination. Of course, for this to be effective, the colour constancy processing must be effective at that scale, and any gains are mitigated by the addition of larger scale results. A multiscale method thus reduces both the chances for success and the chances of failure. In fact, failure is more likely, and in [JRW97] the authors report that the method typically makes the output too grey, due to failures in the grey world assumption which is implicit in the method. This problem is addressed by an unusual, and unfortunately, not well motivated method to put back some of the colour removed by the first stage of processing. The overall method is thus far removed from the theme of this survey, which is illumination modeling.

Modeling scene illumination is an important problem in computer vision. This claim is supported by the existence of a large body of work addressing this problem. This work has lead to improvements in image understanding, object recognition, image indexing, image reproduction, and image enhancement. Nonetheless, much more work is required. One main problem is the development of algorithms for real image data. Most of the algorithms discussed above have quite specific requirements for good results, and those requirements are not met in most real images. Furthermore, even if the requirements are met, they are not verifiable. Preliminary work suggests that the key to progress is better overall models which include more of the physical processes which impact the images. For example, by modeling varying illumination, algorithms have been developed which are not only robust with respect to varying illumination, but can use the varying illumination for better performance. The same applies to specular reflection. Models for real images must be comprehensive, because we cannot always rely on the existence of certain clues such as varying illumination or specularities. Furthermore, both these cases have connections to other computer vision problems such as segmentation and determining scene geometry from image data. Invariably, progress in these areas both aids modeling the scene illumination, and is aided by modeling the scene illumination. Thus there are great opportunities for progress using more sophisticated and comprehensive physics bases models of the interaction of scene with illumination.