a priority queue implementing a stochastic extract-near-min method More...

#include <stoprique.h>

Inheritance diagram for kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >:

Public Types
enum	{ BAD_LOC = 0 }

typedef SATELLITE_TYPE	Sat_tp
	alias of satellite type More...

typedef DijkstraPriorityQueue < SATELLITE_TYPE >::Key_tp	Key_tp
	alias of key type More...

typedef DijkstraPriorityQueue < SATELLITE_TYPE >::Loc_tp	Loc_tp
	alias of locator type More...

Public Types inherited from kjb::qd::DijkstraPriorityQueue< SATELLITE_TYPE >
typedef SATELLITE_TYPE	Sat_tp
	type of satellite data More...

typedef float	Key_tp
	type that we use for keys More...

typedef size_t	Loc_tp
	type that we use for locators More...

Public Member Functions
size_t	size () const
	return the number of (valid) entries in the queue More...

bool	is_empty () const
	predicate tests whether the queue contains no entries More...

void	clear ()
	throw away all contents More...

Loc_tp	ins_max_key (const Sat_tp &sat)
	insert a key with infinite energy (must be relaxed before drawn) More...

Loc_tp	insert (const Key_tp &energy, const Sat_tp &sat)
	insert a key with a given energy and a given satellite value More...

bool	access_loc (Loc_tp spqloc, Key_tp energy, Sat_tp serialnum) const
	fetch the energy or satellite values of indicated record More...

bool	erase_loc (Loc_tp spqloc)
	remove the indicated record More...

bool	rekey_loc (Loc_tp spqloc, const Key_tp &newenergy)
	change the energy of the indicated record More...

Loc_tp	low_energy_sample () const
	get the locator of a record drawn by our devious method More...

Loc_tp	loc_min () const
	get the locator of the record with maximum probability weight More...

Loc_tp	Dijkstra_extraction () const
	method to make this and deterministic pri queue share interface More...

Public Member Functions inherited from kjb::qd::DijkstraPriorityQueue< SATELLITE_TYPE >
virtual	~DijkstraPriorityQueue ()
	obligatory virtual destructor More...

Static Public Member Functions
static Key_tp	power_law ()
	parameter used in the energy ~ probability weight relation More...

Detailed Description

template<typename SATELLITE_TYPE, int POWERLAW_NUM, int POWERLAW_DEN>
class kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >

a priority queue implementing a stochastic extract-near-min method

The idea is to use this in an unsuspecting implementation of Dijkstra's algorithm, but the extract_min() method, via proxy Dijkstra_extraction(), shall not always really return (a locator to) the min. Instead it returns (a locator to) an element at or near the min, drawn according to an empirical discrete probability distribution.

This empirical discrete probability distribution translates distances in the graph (called "energy," since it represents the energy required to travel all that distance) into a discrete non-normalized probability which I call a "weight," since the the stochastic draw is not uniform but is weighted, i.e., it prefers an element with high weight to an element with low weight. The actual frequentist probability of an element is equal to its weight divided by the sum of all weights of elements.

This data structure also supports the idea of zero-energy and infinite-energy elements. These elements are stored in separate trees from the tree that stores positive, finite-energy elements. Infinite-energy elements are the vertices in Dijkstra's algorithm in the time period of the computation before their distance is "relaxed." Zero-energy elements include the source vertex and any vertex that can be reached from the source by traversing zero-distance edges. Such elements are deterministically drawn from the queue (in undefined order) before any positive-weight elements. In a graph with edges that are always positive, the only zero-energy element is the source vertex, on the very first iteration.

Implementation notes

Transform of energy to probability weight

The BIG QUESTION is how to transform positive energy into probability weight 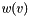$ w(v) $ for vertex 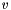$ v $ . If you want behavior similar to a deterministic queue, it should be something like an inverse relationship: if vertices 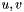$ u,v $ have energies 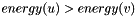$ energy(u) > energy(v) $ , then it should be true that 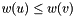$w(u) \le w(v)$ , i.e., 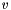$ v $ should have a probability weight no less than that of 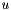$ u $ , so it should at least as likely to be drawn. Empirically there are three obvious choices:

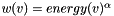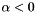an inverse power law: $w(v) = energy(v)^{\alpha}$ for $\alpha < 0$ , e.g., -1.5.
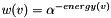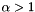an exponential decay: $w(v) = \alpha ^{-energy(v)}$ for $\alpha > 1$ , e.g., 1.01.
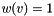a uniform distribution: . I have not tried this but it is feasible. An earlier implementation required that the transform be inverible, but that constraint is gone now.

In implementation, alpha (for either model) is expressed as a rational number with numerator POWERLAW_NUM and denominator POWERLAW_DEN. Another alternative is to just use a uniform distribution, but that is going to look rather different from a shortest path.

Intuition suggests that the polynomial decay will become too uniform for distances far from the source, where the enqueued elements are all a large and almost uniform from the source and the differences among weights is small in comparison. Intuition also suggests that exponential decay could be just too aggressive, period.

Experimentally I've tried power-law decay with alphas of -1.5 and -10. The former has worked alright, whereas the latter has somehow caused strange single-source-short-path trees to form: the destination node apparently wasn't drawn until much later than it should have been, and the resulting path is pathologically (lol) long. So I would avoid large values of 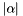$|\alpha|$ .

Experimentally, with exponential decay a modest alpha of 1.01 (1% deflation) has worked similarly to the OK results just mentioned, but alpha of 1.10 (or, 10% deflation) has caused pathological results qualitatively like what I described in the previous paragraph.

I have also considered the idea of adding to the discrete distribution an extra spike of 0.5 to the min-energy/max-weight element, so that the shortest path has a higher density (although the probability of getting the truly shortest path in a big graph is still exponentially tiny). See method Dijkstra_extraction(). The extra spike does not need to be 0.5 of course, but I don't know the best value, but (again going from intuition) that should stabilize the output, i.e., reduce pathlogical behavior. We might even discover that the best behavior is to FORGET about a fancy energy-to-weight function and just go with a uniform probability distribution plus a spike at minimum energy. That would have an attractive simplicity.

Earlier implementations of this class had to deal with zero energy inputs nicely, but that is no longer the case now that we support an "alwaysland" subqueue. Also, an earlier implementation required that the energy2weight function be invertible, but that is no longer a requirement, although the function might still happen to be invertible.

Sub-queues

This queue comprises three sub-queues. When you do a Dijkstra_extract operation, we always draw from "alwaysland," unless it is empty. It hold elements of zero energy. All elements are equally worthy to be drawn. If alwaysland is empty, we draw from "sometimesland," which holds elements of positive energy. The choice is stochastic and depends on the energy of the element, preferring smaller energies. We never draw elements from "neverland," which contains elements that have infinite energy. Elements can be rekeyed and consequently move from one sub-queue to another.

Member Typedef Documentation

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

typedef DijkstraPriorityQueue< SATELLITE_TYPE >::Key_tp kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::Key_tp

alias of key type

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

typedef DijkstraPriorityQueue< SATELLITE_TYPE >::Loc_tp kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::Loc_tp

alias of locator type

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

typedef SATELLITE_TYPE kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::Sat_tp

alias of satellite type

Member Enumeration Documentation

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

anonymous enum

Enumerator
BAD_LOC	a good external locator is always positive, this isn't

Member Function Documentation

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

bool kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::access_loc	(	Loc_tp	spqloc,
		Key_tp *	energy,
		Sat_tp *	serialnum
	)		const

inlinevirtual

fetch the energy or satellite values of indicated record

Implements kjb::qd::DijkstraPriorityQueue< SATELLITE_TYPE >.

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

void kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::clear ( )

inlinevirtual

throw away all contents

Implements kjb::qd::DijkstraPriorityQueue< SATELLITE_TYPE >.

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

Loc_tp kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::Dijkstra_extraction ( ) const

inlinevirtual

method to make this and deterministic pri queue share interface

Returns: locator of node chosen to be removed

I have two lines of code below, only one of which is selected:

return low_energy_sample(); // 1

return kjb_c::kjb_rand() < 0.5 ? low_energy_sample() : loc_min(); // 2

Line 1 relies entirely on its probability weight function. Line 2 takes half the "mass" out of that function and grants it to the max-weight member, so it has a better-than-even chance of being chosen. So when line 2 is active and 1 is disabled, Dijkstra's algorithm with this queue acts much more "calm"; whereas when line 1 is active and line 2 is disabled, Dijkstra's algorithm with this queue is more "adventurous." It turns out that the "adventurous" behavior seems to work better for trails.

The method name is a misnomer; it does not reduce the queue size.

See Also: Transform of energy to probability weight

Implements kjb::qd::DijkstraPriorityQueue< SATELLITE_TYPE >.

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

bool kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::erase_loc ( Loc_tp spqloc )

inlinevirtual

remove the indicated record

Implements kjb::qd::DijkstraPriorityQueue< SATELLITE_TYPE >.

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

Loc_tp kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::ins_max_key ( const Sat_tp & sat )

inlinevirtual

insert a key with infinite energy (must be relaxed before drawn)

Implements kjb::qd::DijkstraPriorityQueue< SATELLITE_TYPE >.

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

Loc_tp kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::insert	(	const Key_tp &	energy,
		const Sat_tp &	sat
	)

inlinevirtual

insert a key with a given energy and a given satellite value

Implements kjb::qd::DijkstraPriorityQueue< SATELLITE_TYPE >.

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

bool kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::is_empty ( ) const

inlinevirtual

predicate tests whether the queue contains no entries

Implements kjb::qd::DijkstraPriorityQueue< SATELLITE_TYPE >.

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

Loc_tp kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::loc_min ( ) const

inline

get the locator of the record with maximum probability weight

Returns: locator of a record with max probability weight.

If the energy-to-weight transform is strictly decreasing, this will be a record with minimum energy (hence the name).

See Also: Transform of energy to probability weight

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

Loc_tp kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::low_energy_sample ( ) const

inline

get the locator of a record drawn by our devious method

Devious method is to give absolute priority to zero-energy records. If any exist (stored in "alwaysland") we return one of their locators, in an undefined order. If none exist, we give stochastic priority to records with finite positive energy (stored in "sometimesland"). We return a locator of a record drawn from empirical discrete distribution defined by the weights of those entries. If ra, rb are both records in sometimesland and if the weight of ra exceeds the weight of rb (equivalently, if the energy of ra is lower than the energy of rb) then ra is more likely to be selected than rb. The exact probability is defined elsewhere (see energy2weight). In this context, the definition of "finite" is loosened up to mean a value less than MAX_ENERGY(), which is a huge number used as a sentinel for infinity.

Records with "infinite" energy (or MAX_ENERGY() energy) are stored but never returned by this method; they are in "neverland."

Returns: locator of the selected record or BAD_LOC if queue is empty.

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

static Key_tp kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::power_law ( )

inlinestatic

parameter used in the energy ~ probability weight relation

Returns: quotient representing the statically-chosen rational number.

If you are using the polynomial decay for the energy~probability xform, value here should be negative (we need increasing energy to have decreasing probability of being drawn from the queue). The magnitude of the value is related to the spread/diffusion of the trajectories. E.g., -1 will cause trajectories to spread "widely," and -20 will cause the trajectories to spread much less. As the value heads towards negative infinity, this data structure will act increasingly like a deterministic priority queue. Large values cause problems. Example: POWERLAW_NUM=-3, POWERLAW_DEN=2 gives decay of order 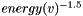$energy(v)^{-1.5}$ , which is reasonable.

If you are using exponential decay, the value here should be positive and a touch above unity, like 1.01 (i.e., POWERLAW_NUM=101, POWERLAW_DEN=100).

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

bool kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::rekey_loc	(	Loc_tp	spqloc,
		const Key_tp &	newenergy
	)

inlinevirtual

change the energy of the indicated record

Implements kjb::qd::DijkstraPriorityQueue< SATELLITE_TYPE >.

template<typename SATELLITE_TYPE , int POWERLAW_NUM, int POWERLAW_DEN>

size_t kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >::size ( ) const

inlinevirtual

return the number of (valid) entries in the queue

Implements kjb::qd::DijkstraPriorityQueue< SATELLITE_TYPE >.

The documentation for this class was generated from the following file:

/work/kobus/src/lib/qd_cpp/stoprique.h

Public Types

Public Member Functions

Static Public Member Functions

Detailed Description

template<typename SATELLITE_TYPE, int POWERLAW_NUM, int POWERLAW_DEN> class kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >

Implementation notes

Transform of energy to probability weight

Sub-queues

Member Typedef Documentation

Member Enumeration Documentation

Member Function Documentation

template<typename SATELLITE_TYPE, int POWERLAW_NUM, int POWERLAW_DEN>
class kjb::qd::StochasticPriorityQueue< SATELLITE_TYPE, POWERLAW_NUM, POWERLAW_DEN >